The Math
To compute points in three space from two-dimensional cameras requires some computations involving linear algebra. To be able to accurately find a point in three space we must be able to see it in two or more cameras image planes. From there it is simply the process of finding the intersection of the vectors coming out of the two cameras image planes going through the world point. This will be explained in more detail below.
We first find the vectors from the cameras focal point to the cameras image plane. This vector simply uses the x, y coordinate of hte point on the image plane, and uses the focal length of the camera (that is the distance from the focal point to the image plane) as its z value. Now that we have these vectors we can see that we have constructed vectors that will intersect the world point. If we only have one camera seeing the point, we have no idea where along that vector the world point will be. If we have two or more on the point, we can calculate the intersection (or the closest point in between the vectors). However, these vectors are in completely different coordinate systems from the world system and eachother, thus we must rotate and translate them into the world system.


First we must set up the room in which we are filming. The layout of the room must follow some important guidelines. You must first determine the world origin in the room, a corner is a good place for this. We must then determine a the axis from the world origin, this is also why a corner is an excelent origin. We can say that the two walls will be our x and y, and the floor can be our z. An image below illustrates this point setup. From there we must find three line parallel to each axis. You can artificially create these by measuring and using markers on the wall, or simply use things along the walls that are parallel to the floor. The points used for these lines must be measured and recorded somewhere, as they will be used later.

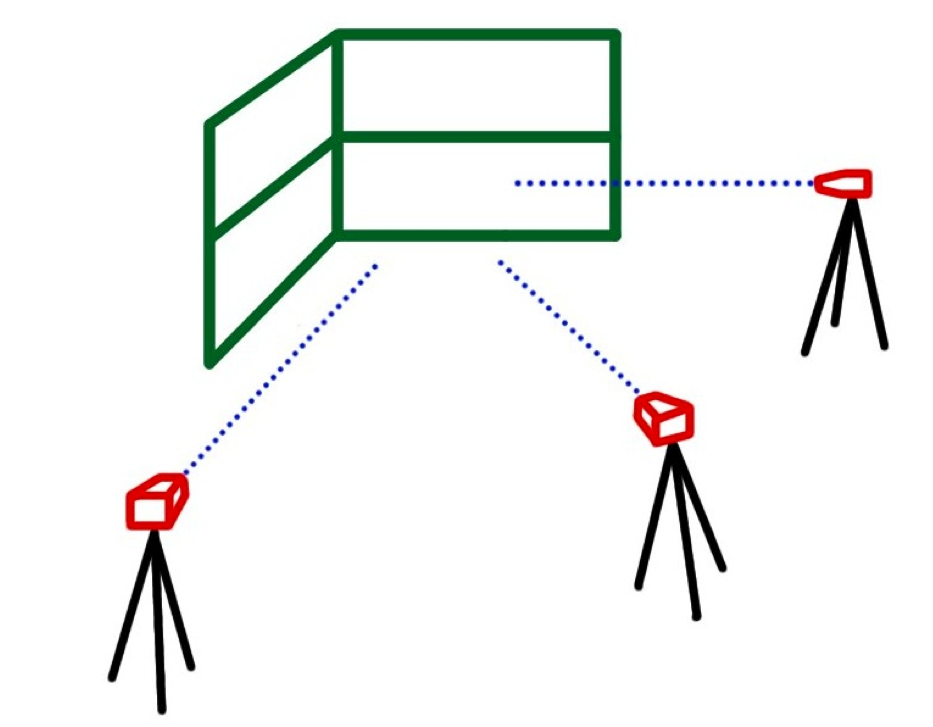
Now that the room setup is complete, we will film using three cameras. From that footage we will calculate the rotation and translation for each camera into the world coordinate system using the known lines and points that we created.
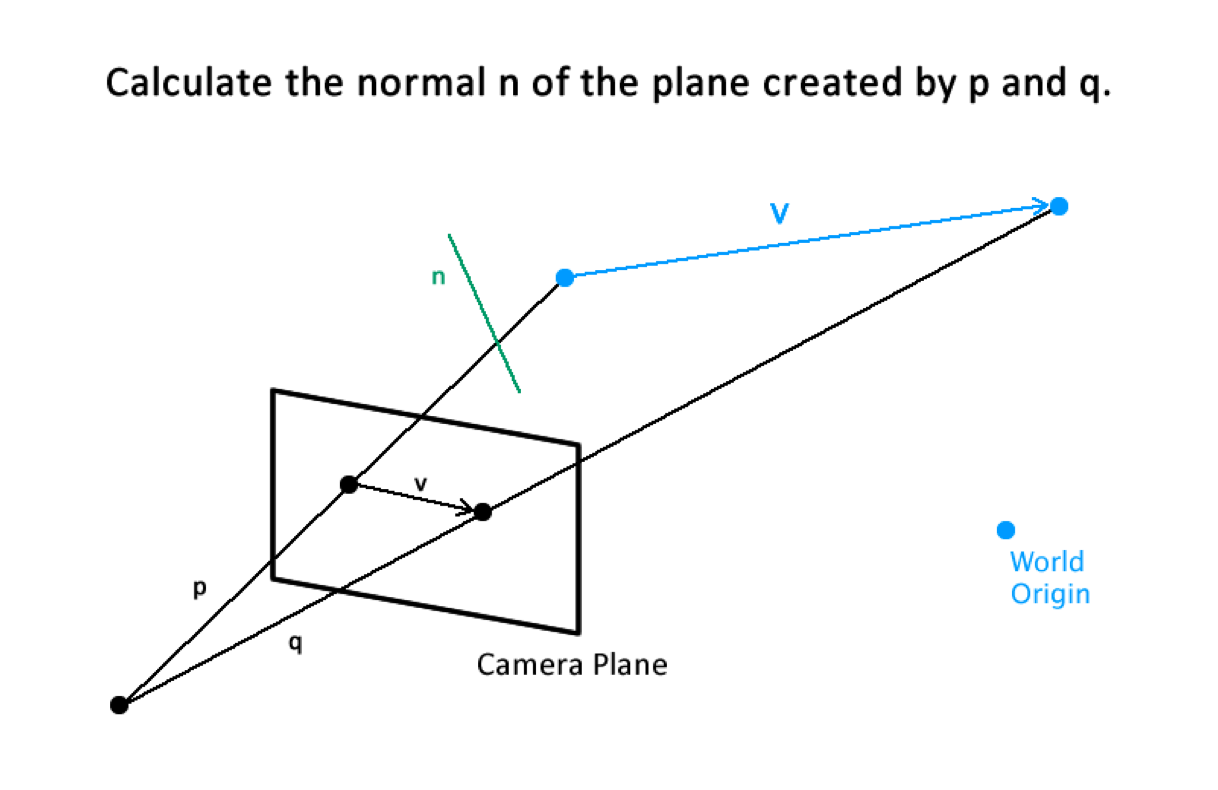
We start out by creating finding the rotation matrix for each camera. This matrix will be apart of the transformation for a world point into the cameras coordinate system. Its inverse will be apart of the process for converting a point in camera coordinates to world coordinates. We start out by calculating the normal of a plane defined by two of the known points the the room. Lets start out by calculation the x-axis rotation. As we can see in the diagram, the vector V is a vector parallel to the x axis and is displayed on the one cameras image plane as the points p and q. These two vectors, p and q, define a plane that we can find the normal of by taking the cross product of the two. Since V times some unknown rotation, call it R, is equal to the projection of V onto the camera plane, call it little v, we can see that R*V will be perpendicular to the normal, n. We can thus form the equation: n . (R*V) = 0, or the dot product of the normal and the rotation times the vector V is equal to 0. Since V is in parallel to the x-axis it is of the form, (s, 0 , 0). Since it only has a value in the first row, when multiplied with R we will only get the first column of R times the length of V. This gives us an equation with only the three unknown values in the first column of R, and since we have three of these lines that are parallel to the x-axis, we get three equation and three unknowns. Thus we just solve for for the first column, and then we repeat for the other two axes.
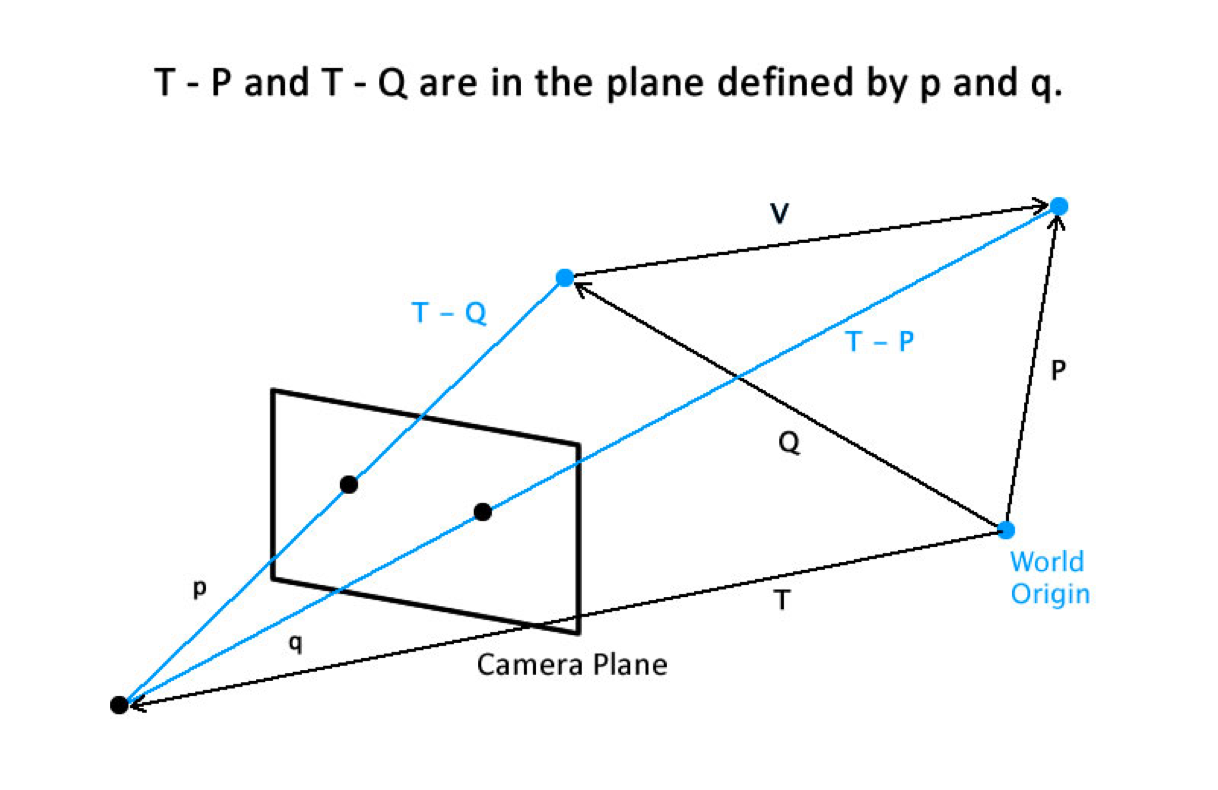
We then find the translation using a very similar process. Since we know the exact location of V in the world (because we measured the two points that define it, lets call them big P and Q), we can use those points and our now known rotation to find the translation. We do this by assuming some translation vector, call it T, that points from the world origin to the cameras focal point. To find out what this T is, we will subtract P and Q from it. We know that T - P, is in the same plane of p and q that we defined before. View the illustration below for a visual representation of this. Since it is in the plane, we can construct a similar equation to before: n . R*(T-P) = 0, we can also do this for Q. We end up with T, with is (t1,t2,t3) times some known coefficients. We can easily get three of these equations, so we solve for the three unknowns.
Now that we have the translation and rotation, we can solve for the intersection of these two vectors c1 and c2. To do this we construct an equation of the form. (T1 - s1(R1^-1*c1)^2 - (T1 - s2(R2^-1*c2)^2 = 0, or the the first camera translation minus its vector towards the world point times the inverse of its R, times some scalar, squared, minus the camera vector under the same translation and rotation equals 0 (because they should be the same world point). We have two unknowns here but only one equation, so we take the derivative of the equation with respect to both s1 and s2 to get two equations of the form: a*s1 + b*s2 = 0, which we can use to solve for s1 an s2. Since we now have this scalar we can plug it back into our equation to get the actual world point.
There is a problem, none of these equations have an exact solution due to measurement errors. To solve for this problem, we do least squares to minimize the equations. For more information on how this was done, please refer to the PDF by Jack Goldfeather.