Shapley's Math

Due to their strong mathematical backing, Shapley values are incredibly widely used in the field, thus they are almost obligatory to include in the project. But how do Shapley values work?

Before we wade into the math, let's establish a quick base: a machine-learning model takes a set of features as input, performs some kind of calculation on them, and returns an output (in our case, a real-valued confidence score in a potential classification). Now that we have this foundation, let's begin.

Intuition - Game Theory

Shapley values have their roots in coalitional game theory. Assume that our machine learning model is a game, where each feature's value is a player, and where the model's output is the final result of the game. Shapley values tell us how each player contributed to the final result of the game.

Suppose each feature values begins to contribute to the game in a random order. The Shapley value for a feature value is the difference between outcomes when the feature value is and isn't playing in the game of prediction.

How do we simulate a feature value "not playing?"

In Shapley's original text, A value for n-person games, a player can simply not join the game until their turn; however, a machine learning model most often takes a fixed number of inputs, and as such a player simply cannot choose to refrain from partaking in the game.

Therefore, we must find a way to pretend that a player is absent. This is one of two places where approaches diverge. In some cases, a value is randomly sampled from an acceptable range or even completely unconstrainedly. Our implementation, in accordance with Cristoph Molnar, accesses random instances from our training data to replace any values which are "not playing."

For images, one of the most efficient methods to simulate a pixel "not playing" is to blur it with a masker, as shown in Applying Shapley to the ResNet network.

What is a coalition?

Since we are working with real-world data, we cannot assume that each feature acts independently of one another. As such, we must simulate prediction across all coalitions of the inputs, where a coalition is a subset of the total feature values working together. For the calculation of Shapley values, this means that when a coalition is considered, all values inside the coalition are a package deal: they either all play, or none of them play, instead of each feature value playing/not playing on an individual basis.

How to approximate Shapley values

The actual calculation of Shapley values requires some heavy integration. As such, we decided to approximate our input's Shapley values with the shap package instead.

As proposed in Štrumbelj et al. (2014), we can approximate a shapley value $\phi_j$ for a feature value $j$ through the calculation:

$$\begin{align} \phi_j = \frac{1}{N} \cdot \sum^N_{n=1}(f(x^n_{+j}) - f(x^n_{-j})) \end{align}$$

Where $f$ is the prediction function for our model, and $x^n$ is a random permutation of the input values playing. As such, this is the average over all possible coalitions of that input with $j$ specifically participating and specifically not participating. Because we should simulate as many coalitions of the input $X$ as possible ($X$'s powerset $\forall x^n \in \mathcal{P}(X)$ ), $N$ should try to approach $|\mathcal{P}(X)|$, or $2^{|X|}$.

We can approximate Shapley $\phi_j$ using the following algorithm.

1. For $N$ coalitions $x^n$ drawn from $\mathcal{P}(X)$:
   Calculate $\phi^n_j = f(x^n_{+j}) - f(x^n_{-j})$, where all feature values in $x^n$ are participating, and where $j$ participates in $x^n_{+j}$, and $j$ abstains in $x^n_{-j}$
2. Compute the average value across all $\phi^n_j$ to get $\phi_j$.

This allows us to not only get the overarching Shapley values for each input, but if we wanted we could draw a single $\phi^n_j$ to see how $j$ factored into coalition $x^n$ specifically.

Basic properties

Four basic properties hold under Shapley values, each of which tell us something about our payout. Let $\phi_j$ represent the Shapley value for feature value $j$, and let $\mathcal{P}(X)$ be all possible coalitions of input $X$:

• Efficiency: All Shapley values must sum to the difference between the prediction on the input and the average prediction.

$$\begin{align} \phi = \sum^{|X|}_{j=1}\phi_j = f(X) - E(f(X)) \end{align}$$

• Symmetry: Features $i$ and $j$ have the same contribution to the prediction if they contribute identically to all coalitions.

$$\begin{align} [\forall x^n \in \mathcal{P}(X) : \phi{^n_i} = \phi^n_j] \implies \phi_i = \phi_j \end{align}$$

• Nullity: If a feature $j$ changes nothing in the prediction in all possible coalitions, then it has a Shapley value of 0:

$$\begin{align} [\forall x^n \in \mathcal{P}(X) : f(x^n_{+j}) = f(x^n_{-j})] \implies \phi_j = 0 \end{align}$$

• Additivity: For a prediction with multiple components $p + p'$, the Shapley values for a feature value $j$ can be represented as:

$$\begin{align} \phi_j + \phi_j' \end{align}$$

Firstly, the efficiency property shows us that this game's outcome was exactly a combination of each contribution, and is thus no more or less than the sum of its parts. From here, symmetry tells us that the contributions must be fairly distributed, as if two features contributed the same amount, they must receive the same payout; this is extended with nullity, as if some feature means literally nothing to the prediction, then it contributed nothing. Finally, additivity tells us that multi-part predictions must also have multi-part contributions, as each feature played some role (even if it is no role) in all parts of the prediction.

What questions can Shapley values answer?

All of this math allows Shapley values to answer two questions, both local to the specific prediction, and both relating to the expected prediction:

1. Shapley values show how a feature value $j$ contributed to the prediction's deviation from the expected prediction, and
2. Due to the calculations of all coalitions, we can also see how a coalition $x \in \mathcal{P}(X)$ contributed to the deviation of $f(X)$ from the expected prediction.

Application of properties: MOOC Dataset

For a detailed look at this dataset's explanations, please see Shapley and MOOC and our Methodology.

A more intuitive application of the additivity property can be seen with our MOOC model. Since our model outputs the probabilities for two binary classes (complete/incomplete), the game of prediction is zero-sum (Since probabilities sum to 1, $+1\%$ chance of "complete" means $-1\%$ chance of "incomplete"). As such, the Shapley values are also zero-sum, as visualized in the picture below:

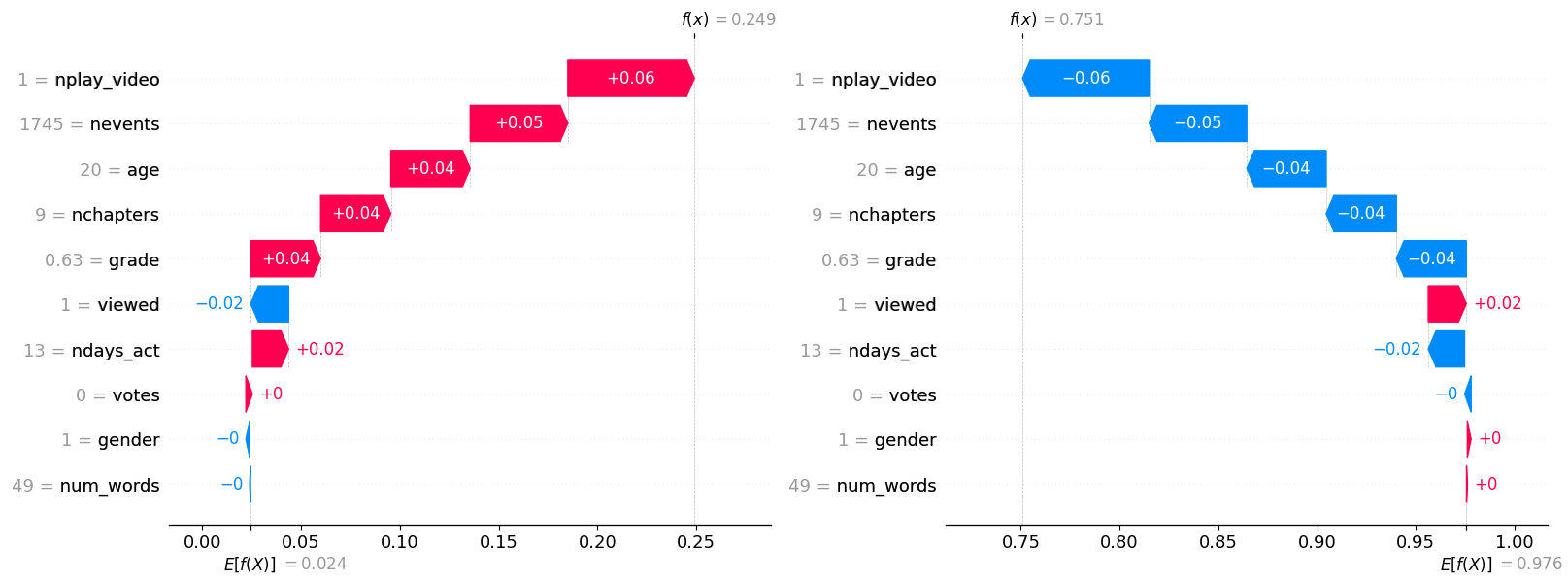
These are the graphs of probability for the classes of "Complete" (left) and "Incomplete" (right). They have expected values $E[f(x)] =$ $0.024$ and $0.976$, respectively, and they end at actual predictions $f(x) =$ $0.249$ and $0.751$, respectively. Both $E[f(x)]$ values sum to 1, and so too do the actual predictions $f(x)$. Because this prediction is a zero-sum game, the Shapley values of the classes are inverses:

$$\begin{align} \phi_{complete}=0.225, \;\;\; \phi_{incomplete}=-0.225 \end{align}$$

Since each Shapley value for a class is itself a combined payout from the contributions of all the feature values, we also see that every Shapley value for each feature is mirrored across classes, such that:

$$\begin{align} \phi_{j:\;complete} = - \phi_{j:\;incomplete} \end{align}$$

We can also intuit the efficiency property here, as the feature values build from $E[f(x)]$ to $f(x)$ perfectly. Similarly, by applying nullity, we can infer that gender contributes approximately nothing to our prediction (we aren't being sexist here, yay!), and we can infer through symmetry that grade, nchapters, and age must contribute approximately the same across all coalitions of feature values.