[Optional Assignment] - Recursion
Due: Wednesday, March 11, 2020, at 5pm
You may work alone or with a partner, but you must type up the code yourself. You may also discuss the assignment at a high level with other students. You should list any student with whom you discussed the assignment, and the manner of discussion (high-level, partner, etc.) in a readme.txt file that you include with your submission.
You should submit your assignment as a .zip file on Moodle.
You will work in one file for this assignment. Download the skeleton code. You should save the code file as recusion.py.
Parts of this assignment:
Note on style:
The following style guidelines are expected moving forward, and will typically constitute 5-10 points of each assignment (out of 100 points).
- Variable names should be clear and easy to understand, should not start with a capital letter, and should only be a single letter when appropriate (usually for
i,j, andkas indices, potentially forxandyas coordinates, and maybepas a point,cfor a circle,rfor a rectangle, etc.). - It’s good to use empty lines to break code into logical chunks.
- Comments should be used for anything complex, and typically for chunks of 3-5 lines of code, but not every line.
- Don’t leave extra print statements in the code, even if you left them commented out.
- Make sure not to have code that computes the right answer by doing extra work (e.g., leaving a computation in a for loop when it could have occurred after the for loop, only once).
- Use lowercase first letters for variables and methods, and uppercase first letters for classes.
Note: The example triangle-drawing program on page 108 of the textbook demonstrates a great use of empty lines and comments, and has very clear variable names. It is a good model to follow for style.
Problem 1: Work smarter, not harder
The straightforward recursive solution to find the nth Fibonacci number has a huge downfall: it re-computes results tons of times. We can mitigate this using “memoization”. The idea is to store the results (for example, in a dictionary), and only compute a result that isn’t already stored.
For this problem, implement the function fasterFibHelper. This function takes as input not only the value n, but also a dictionary called memo that maps input numbers to Fibonacci numbers. For example, this dictionary might at some point contain the following key-value pairs: {1: 1, 2:1, 3: 2, 4: 3, 5: 5, 6: 8}.
def fasterFibHelper(n, memo):
"""
If n is a key in memo, returns the stored result.
Otherwise, computes fib(n) and stores the result in memo
before returning it.
"""
return 0 # TODOMake sure that this function has the usual base case(s) for Fibonacci, and that it either returns a value from memo, or stores a value in memo before returning even for the base case(s).
You can test your function by calling fasterFib(35). You should get the value 9227465. However, fasterFib(35) should return almost instantly, whereas fib(35) might take 5-10 seconds (or more!) to complete.
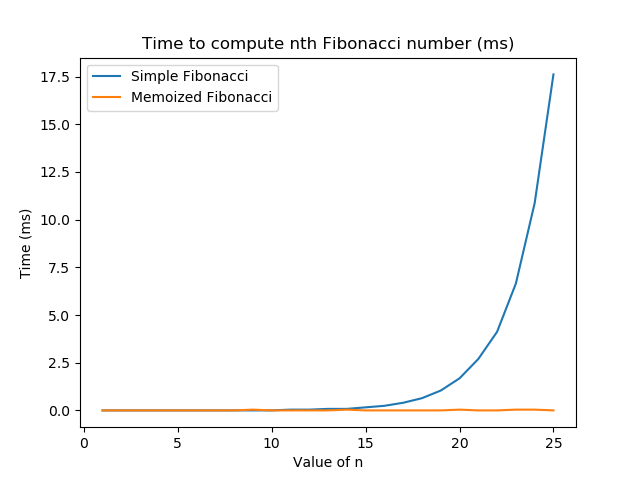
Problem 2: Plotting runtimes of Fibonacci
For this problem, you should measure the runtimes of both fib and fasterFib. To do this, you should time 100 function calls to each, for n from 1 to 25, and take the average runtime. Take a look at exercises from lesson 24 and lesson 26 for examples of measuring runtimes.
Implement the timing and plotting in the function timeFib.
def timeFib():
pass # TODOYour resulting plot should look like the following:
What you should submit
You should submit a single .zip file on Moodle. It should contain the following files:
readme.txt(collaboration statement listing collaborators and form of collaboration)recursion.py(both problems)