Due: Wednesday, February 12, 2020, at 1:50pm

This assignment is completely optional. If you receive at least 80% of the points, you will gain one extra late day. If you receive at least 50% of the points (but not quite 80%), you will gain half of an extra late day.

You may work alone or with a partner, but you must type up the code yourself. You may also discuss the assignment at a high level with other students. You should list any student with whom you discussed the assignment, and the manner of discussion (high-level, partner, etc.) in a readme.txt file that you include with your submission.

You should submit your assignment as a .zip file on Moodle.

Parts of this assignment:

• Problem 1: Testing for N-Rooks
• Problem 2: Testing for N-Queens

Getting started

This assignment comes with starter code. You can copy-paste it into a window in IDLE – just save it as verifyNQueens.py.

You will implement two functions in this assignment. The rest of the file is code to help test your implementations. Try running it to see what tests it will perform:

Performing positive N-Rooks tests.
Passed 0 out of 100 tests (n=0).
Passed 0 out of 100 tests (n=1).
Passed 0 out of 100 tests (n=2).
Passed 0 out of 100 tests (n=3).
Passed 0 out of 100 tests (n=4).
Passed 0 out of 100 tests (n=5).
Passed 0 out of 100 tests (n=6).
...

Problem 1: N-Rooks

In this problem, you will implement a function that checks if a given board state satisfies the “N-Rooks” problem. That is, it checks whether no two pieces are in the same row or column (and thus whether they’d threaten each other if they were rooks in a game of chess).

The board state is represented as a list of lists (another nested list). The function doesSatisfyNRooks takes a parameter boardState that contains one list per row. Each inner list contains one value per cell within that row. The value is 0 if no piece is placed there, and 1 if there is a piece placed there.

def doesSatisfyNRooks(boardState):
    """
    Checks whether the given state of the board satisfies N-Rooks.
    If no two pieces are in the same row or column, returns True.
    Otherwise, returns False.

    boardState: a nested lists containing 0s (no piece) or 1s (a piece)
    
    returns: True or False
    """
    # TODO: Problem 1
    return False # replace with your code

This assignment comes with some tests that will help you verify your code works. Although you don’t have to fully understand how the tests work, they can be helpful for getting a feel for the expected results.

Once you have implemented doesSatisfyNRooks, the first two tests should pass. The positive tests will all pass, but the negative tests will pass more frequently with increasing n. This is because the negative tests randomly generate a board setup, and it might satisfy N-Rooks, but this becomes less likely as the board becomes larger.

Performing positive N-Rooks tests.
Passed 100 out of 100 tests (n=0).
Passed 100 out of 100 tests (n=1).
Passed 100 out of 100 tests (n=2).
Passed 100 out of 100 tests (n=3).
Passed 100 out of 100 tests (n=4).
Passed 100 out of 100 tests (n=5).
Passed 100 out of 100 tests (n=6).
Passed 100 out of 100 tests (n=7).
Passed 100 out of 100 tests (n=8).
Passed 100 out of 100 tests (n=9).
Passed 100 out of 100 tests (n=10).

Performing negative N-Rooks tests.
(Note that not all will pass, but the number should go up as n increases.)
Passed 0 out of 100 tests (n=0).
Passed 0 out of 100 tests (n=1).
Passed 39 out of 100 tests (n=2).
Passed 75 out of 100 tests (n=3).
Passed 91 out of 100 tests (n=4).
Passed 98 out of 100 tests (n=5).
Passed 99 out of 100 tests (n=6).
Passed 100 out of 100 tests (n=7).
Passed 100 out of 100 tests (n=8).
Passed 100 out of 100 tests (n=9).
Passed 100 out of 100 tests (n=10).

Problem 2: N-Queens

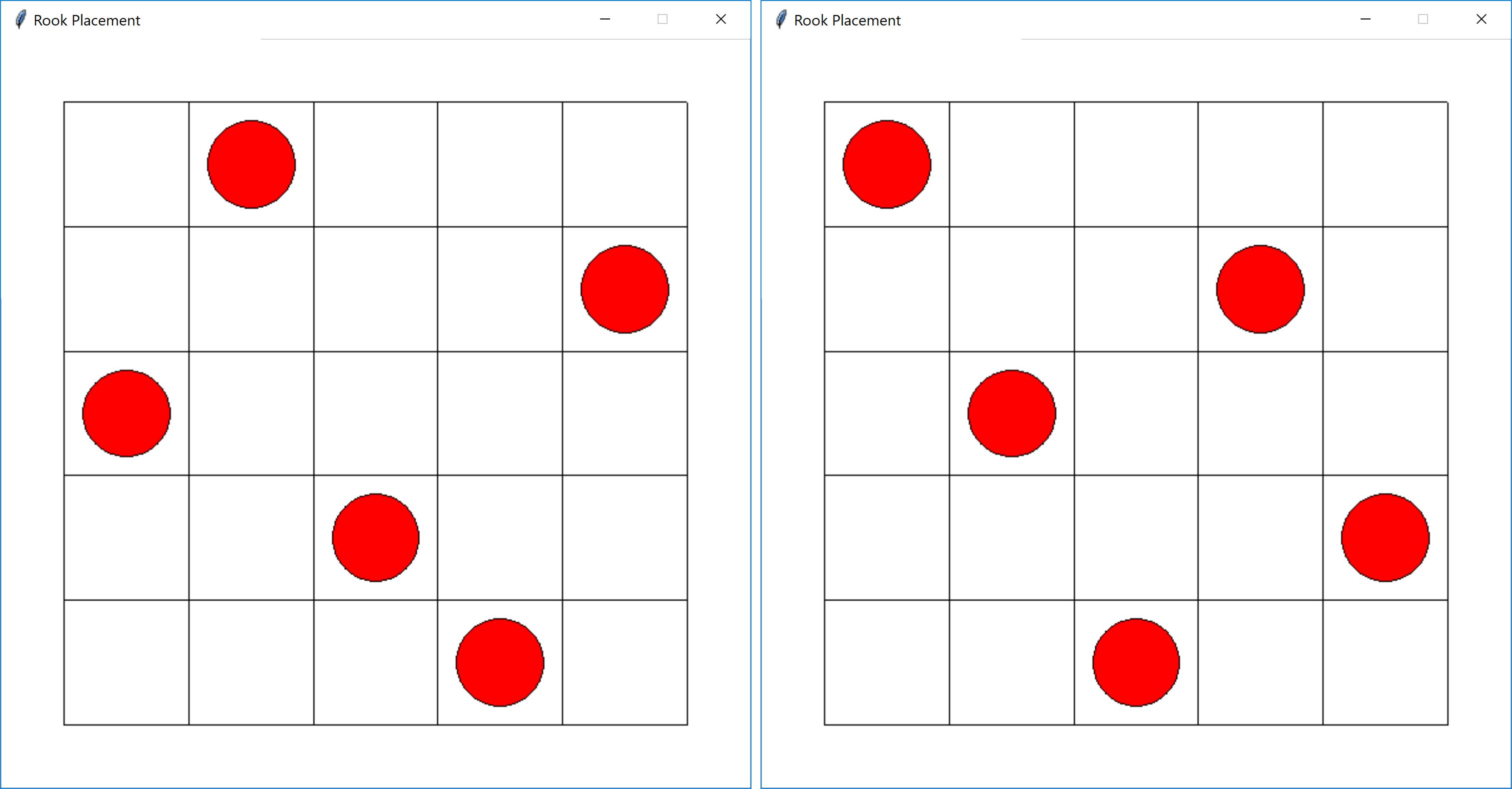
For this problem, you will implement the function doesSatisfyNQueens. The logic for this problem is a bit more complex. The function should only return True if no two pieces are placed in the same row, column, or diagonal.

For example, the board state on the left below would satisfy N-Queens, as the bottom two pieces are in the same diagonal. However, the board state on the right would satisfy N-Queens.

def doesSatisfyNQueens(boardState):
    """
    Checks whether the given state of the board satisfies N-Queens.
    If no two pieces are in the same row, column, or diagonal,
    returns True.  Otherwise, returns False.

    boardState: a nested lists containing 0s (no piece) or 1s (a piece)
    
    returns: True or False
    """
    # TODO: Problem 2
    return False # replace with your code

Again, there are test functions available to help you verify your code works. As with N-Rooks, the positive tests for N-Queens should all pass. The negative tests all generate random board configurations, and assume it is unlikely that they will pass N-Queens. Therefore, more will pass as n increases.

Note: There was a bug in my code that resulted in two of the positive tests for N-Queens being invalid. This is fixed in the updated starter code.

Performing positive N-Queens tests.
Passed 1 out of 1 test (n=0).
Passed 1 out of 1 test (n=1).
Passed 1 out of 1 test (n=2).
Passed 1 out of 1 test (n=3).
Passed 1 out of 1 test (n=4).
Passed 1 out of 1 test (n=5).
Passed 1 out of 1 test (n=6).
Passed 1 out of 1 test (n=7).
Passed 1 out of 1 test (n=8).
Passed 1 out of 1 test (n=9).
Passed 1 out of 1 test (n=10).

Performing negative N-Queens tests (assuming N-Rooks passes).
(Note that not all will pass, but the number should go up as n increases.)
Passed 0 out of 100 tests (n=0).
Passed 0 out of 100 tests (n=1).
Passed 51 out of 100 tests (n=2).
Passed 53 out of 100 tests (n=3).
Passed 83 out of 100 tests (n=4).
Passed 80 out of 100 tests (n=5).
Passed 85 out of 100 tests (n=6).
Passed 98 out of 100 tests (n=7).
Passed 97 out of 100 tests (n=8).
Passed 97 out of 100 tests (n=9).
Passed 100 out of 100 tests (n=10).

Performing negative N-Queens tests (likely fails N-Rooks).
(Note that not all will pass, but the number should go up as n increases.)
Passed 0 out of 100 tests (n=0).
Passed 0 out of 100 tests (n=1).
Passed 58 out of 100 tests (n=2).
Passed 83 out of 100 tests (n=3).
Passed 100 out of 100 tests (n=4).
Passed 100 out of 100 tests (n=5).
Passed 100 out of 100 tests (n=6).
Passed 100 out of 100 tests (n=7).
Passed 100 out of 100 tests (n=8).
Passed 100 out of 100 tests (n=9).
Passed 100 out of 100 tests (n=10).

What you should submit

You should submit a single .zip file on Moodle. It should contain the following files:

• readme.txt (collaboration statement listing collaborators and form of collaboration)
  
• verifyNQueens.py (both problems)