Robotics: Manipulation Assignment

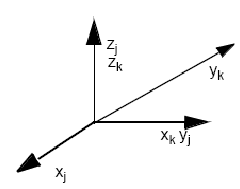
If the origins of two coordinate frames are on top of each other (for example, after a rotation), you should draw the two frames right on top of each other. This may result in some axes having two labels, as in the image here. Be sure to draw it first on scrap paper first so that your final drawing is neat.

Problem A

For each part, draw and label the axes. When you are done with this question, you should have 5 different coordinate frames drawn and labeled.

1. Draw a 3-D coordinate frame where x points up and y points to the right. We�ll call this a-coordinates. Label the axes x_a, y_a, and z_a.
2. Transform the a frame into the b frame by doing a Trans(3, 4, 0) (relative to a�s coordinates) (label the axes!)
3. Rotate the frame by 90 degrees about b�s y axis and draw the resulting coordinate frame (call it c and label the axes.)
4. Translate the frame by (3,4,0) (relative to c�s coordinates) and draw the resulting coordinate frame (call it d and label the axes).
5. Rotate the frame by -180 degrees about d�s x axis and draw the resulting coordinate frame (call it e and label the axes).
6. Using just Trans and Rot operators (i.e. do NOT compute the matrices) describe the transformation that will take a point in e coordinates and transform it to a point in a coordinates (in other words, I�m looking for a bunch of Trans and Rots multiplied together)
7. To compute this transformation, did we use “moving” or “fixed” coordinates?

Problem B

For each part, draw and label the axes. When you are done this question, you should have 4 different coordinate frames drawn and labelled.

1. Draw a brand new 3-D coordinate frame where x points down, and y points to the left. Label the axes x_h, y_h, and z_h.
2. Transform the h frame into the i frame by doing a Trans (0,3,0) (relative to h�s coordinates)
3. Rotate the i frame by -90 degrees about h�s z axis and draw the resulting coordinate frame (call it j). IMPORTANT NOTE: This is a “fixed axes” interpretation of the world, and we haven't done an example quite like this in class (a rotation about the original coordinate system after we have translated the coordinate system away). This is a fairly difficult rotation to get right. To do it correctly, pretend that the h and i frames are locked together in space before you start the rotation so that your new j frame ends up in the right place.
4. Transform the j frame into the k frame by doing a trans (2,0,0) (relative to the original h coordinate frame. Remember, the orientation and position of the h coordinate frame should still have not changed regardless of the previous steps.)
5. Using just Trans and Rot operators (i.e. do NOT compute the matrices) describe the transformation that will take a point in k coordinates and transform it to a point in h coordinates.
6. Compute the matrix that corresponds to your answer in the previous part.
7. Now consider your two coordinate frames h and k. Using “moving” coordinates, and just Trans and Rot operators, describe the transformation that will take a point in k coordinates and transform it into a point in h coordinates. NOTE: You are going to have to think about what transformations you need to get between the two axes when you�re using moving coordinates instead of the fixed ones we used in steps h through k.
8. Compute the matrix that corresponds to your answer in the previous part. If it�s not the same as your answer for “fixed axes,” something is wrong!

Problem C

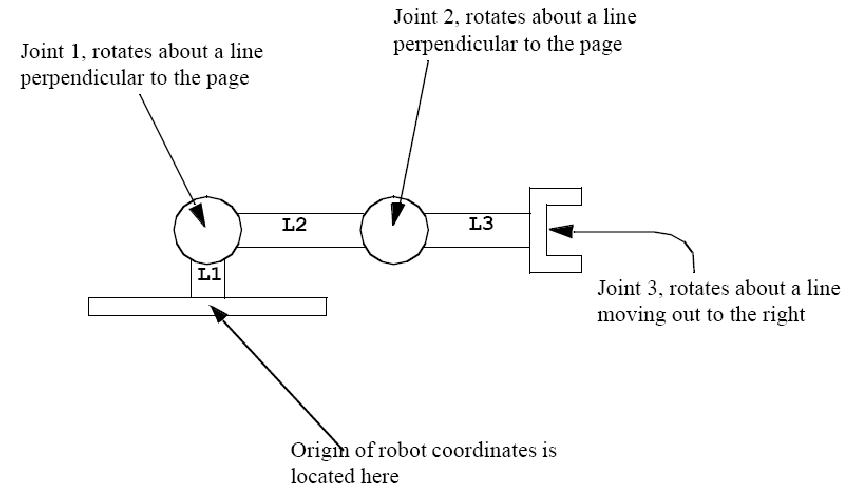
Assume that you have a robot whose initial position is as depicted above, with 3 joints and 3 links as detailed above.

Wherever appropriate, feel free to use either Octave or Mathematica. You may turn in a printout from either tool, but make sure that whatever you turn in is clean and readable.

1. Redraw the robot with axes labelled (when I did this assignment I had four different coordinate frames). Assume that the robot coordinate frame has x pointing up and y pointing to the right. Also assume that gripper coordinates (with origin at the center of joint 3) has z pointing straight out of the gripper (to the right in the picture) and x pointing out of the paper in the picture.
2. Suppose the length of Link 1 is 10 cm, Link 2 is 20 cm, and Link 3 is 15 cm. Compute the transformation matrix that takes a point in gripper coordinates to a point in world coordinates when the arm is pointing straight up, with Joint 3 rotated by 90 degrees. Use this matrix to convert the point (0, 0, 0) in gripper coordinates into world coordinates. (Hint: visually check your answer, if it looks right, there�s a good chance your matrix is right.)
3. Suppose the length of Link 1 is 12 cm, Link 2 is 34 cm, and Link 3 is 8 cm. Compute the transformation matrix that takes a point in gripper coordinates to a point in world coordinates when joint 1 is rotated in such a way that the arm is pointing straight out to the left. Joints 2 and 3 should be unrotated. Use this matrix to convert the point (0, 0, 0) in gripper coordinates into world coordinates.