CS 111: Introduction to Computer Science

Fractal squares

Due: 11:59PM Monday, November 9. Hand in as squares.py.

When you're first learning about recursion, you spend a lot of time with little problems like computing factorials, reversing strings, etc. All of these problems can be solved pretty easily using loops, so a skeptic might say "recursion is cool, but why bother?"

Here's why. Some important problems are so naturally recursive that most people find it effectively impossible to solve them in a non-recursive way. For example, suppose you wanted to print out the complete list of all the permutations of a set (i.e. all the different ways you can order the elements of the set). If, say, your set is {goat, moose, emu}, then your permutations would be:

goat moose emu goat emu moose moose goat emu moose emu goat emu goat moose emu moose goat

Permuting a set is tricky with recursion, but the resulting code is just a few lines long. Permuting a set without recursion--well, let me just encourage you to think about how you would go about it.

Another naturally recursive problem is the drawing of fractals--images that are identical or nearly identical to a sub-part of themselves. For a classic example of a fractal, take a look at Sierpinski's Triangle. If you look at just one corner of the full Sierpinski's triangle, what you see is another Sierpinski's triangle--just a little smaller. As with all recursive algorithms, you solve the big problem ("draw Sierpinski's triangle") by breaking it into smaller problems of the same type ("draw three Sierpinski's triangles of half the height of the big one").

The program sierpinski.py illustrates the kind of recursive technique you can use to draw Sierpinski's triangle. Your job for this assignment will be to adapt these techniques to draw the figure below:

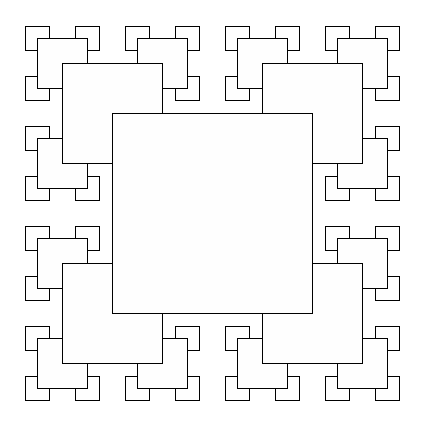
More specifically, your program should obtain from the user the number of "levels" of squares (the number of different sizes of squares) to draw, and then draw the corresponding image. The example above has 4 levels of squares. The examples below have 2, 3, and 5 levels of squares, respectively.

Have fun.