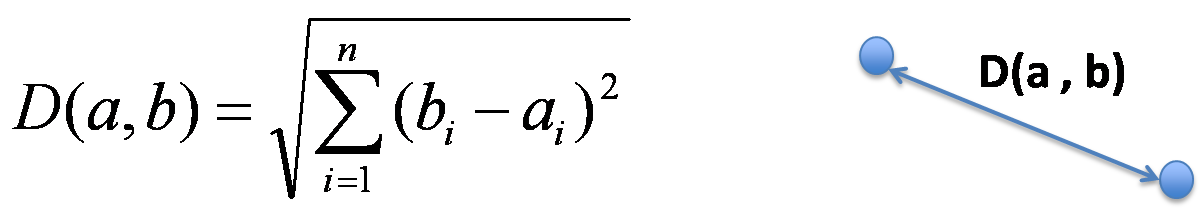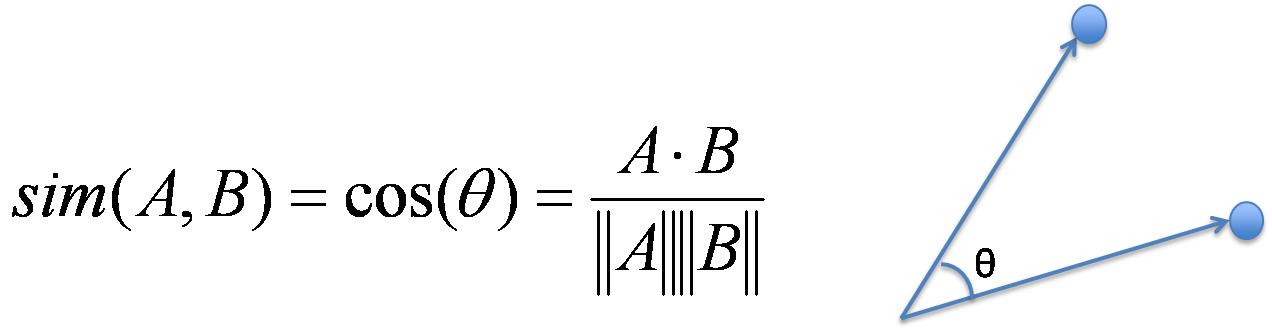k Nearest Neighbor algorithm is a very basic common approach for implementing the recommendation system. In k Nearest Neighbors, we try to find the most similar k number of users as nearest neighbors to a given user, and predict ratings of the user for a given movie according to the information of the selected neighbors. So the algorithm has a lot of variation based on two points. One is how to calculate the distance of each user, and another is how to use or analyze the nearest neighbors to predict the ratings of a given user. I implemented Euclidean Distance and Cosine Similarity as the methods to calculate the distance, and tried various ways of analysis to predict the ratings like taking average, weighted average or the majority among nearest neighbors.

Now I explain a little about the methods of measuring the distance. First, Euclidean Distance is the ordinary straight line distance between two points in Euclidean Space. If the dimension is two, the distance is just between two points in xy plane space, and we just extend this concept to use for our 17,000 dimensional space to calculate the length of the line.

On the other hand, Cosine Similarity is the measure of calculating the difference of angle between two vectors. Becasue the length of the vector is not matter here, I first normalize each vector to a unit vector, and calculate the inner product of two vectors.

After I implemented cosine similarity algorithm, I notice one problem. Because the dataset we have is highly sparse, it's very rare that two users have commonly rated movies. If a given user has no users among potential candidates of nearest neighbors, who rated the same movie, all cosine similarity become 0, and we cannot figure out which users are the nearest neighbors. For avoiding this situation, I set default values for missing ratings. It means that usual ratings are between 1 and 5, but if a user does not rate a movie, I set very small value like 0.1 instead of 0. As the result of this process, I can get nearest neighbors in all cases.

Here is the result of the three methods.

The error of cosine similarity is just among ratings who are ruturned by system. So there are a lot of cases where the system do not return the predcted ratings as I expalined now. As you can see, Euclidean distance is the worst one. And also, I found that even when we set non-zero default values for missing ratings, the performance of the prediction is very close. Because I can get all predicted ratings when I set non-zero default values, I think cosine similarity with default values is the best algorithm among these three methods.

However, the error is still larger than 1.1, which implies that it is not the efficient way of predicting ratings. So I think about why the error is still big.

What I think as one of the reasons is that there is an local minimum issue in my implementation. It means that selected nearest neighbors are not the actual nearest neighbors, but just neighbors among some partial users. Because of the time and memory consuming issue, I consider only users who rates a given movie. Here is the virtual visualization of the distance of each user who rates a given movie as a adjacency graph.

In this case consider I need to know the nearest neighbors of a user like Professor Dave. In this graph, this another user, named College Dave, seems far away from Professor Dave. But if we combine the other user groups which rates very similar movies to a given movie, we can consider more large number of users.

And in that case, the distance between Professor Dave and College Dave is changed and the nearest neighbors are also changed.

For considering this local minimum problem, I used dimensionality reduction technique. I combined similar movies together, and as the result I can consider more larger number of users to select nearest neighbors. I reduced dimension from 17,000 to 100.

For actual process of dimensionality reduction, I use one algorithm named LPP.

There are three steps for using LPP.

• First I created an adjacency graph like the previous slide. This process is the approximation of the distance between each user.
• I chose weights for all edges between users.
• And finally, I compute the eigenvectors from the equation here.

I use this calculated eigenvectors to reduce the dimension of original matrix of X.

Here is the final result of dimensionality reduction technique.

when k=15, and final dimension=100, the RMSE becomes 1.060185. Comparing to other algorithms when k=15, this algorithm has the best performance because each RMSE when k=15 is 1.173049, 1.147835, 1.148560 in Euclidean, cosine similarity and cosine similarity with default values respectively.

As you can see, the RMSE after dimensionality reduction becomes smaller than any of other methods. It improved about 10% from others. However, it's still larger than 1.0, and it suggests that k Nearest neighbor algorithm has a limitation for predicting ratings. I think one of the reason of this inefficiency is that k Nearest neighbor algorithm needs to rely on the actual information of specific users, and in the case of sparse matrix, the gap between a given user and nearest neighbors becomes large.